The technique is a common approach used in programming to swap the positions of two values. It involves the use of a temporary variable as an intermediate storage space.

To perform the swap, you follow these steps:

1. Take the second of the values and assign it to the temporary/auxiliary variable. This ensures that the value is not lost during the swapping process.
2. Assign the first value to the position of the second value.
3. Finally, assign the value stored in the temporary/auxiliary variable to the position of the first value.

By using this technique, the values effectively exchange their positions without the risk of losing any data. This technique ensures that the swap is done safely and efficiently.

This technique finds extensive application in sorting algorithms, where reordering elements is a common operation. It is also useful in various other algorithms where value swapping is necessary.

Example:

This technique is used in sorting algorithms, such as the bubble sort. To illustrate the use of Swap with Auxiliary Variable, let’s consider a list of elements (6, 3, 5, 5, 2 and 4). Our goal is to move the largest number to the leftmost position in the list. That in this case it will be the 6.

We start comparing the values to utilize this technique. In this case, we will compare two adjacent values of the list from the begging of the list, such as 6 and 3, as we examine them, we need to move the 6 to the left and the 3 to the right.

In this technique, the step 1, says we need to take one value and assign it to the temporary/auxiliary variable. So we took the second value the number 3 and assign to the auxiliary variable.

Then, in the step 2, says that we need to assign the first value, which is the number 6 in this case, to the position where the second value (the number 3) was stored. It may seem like we lost the number 3, but we have safely stored in the auxiliary variable.

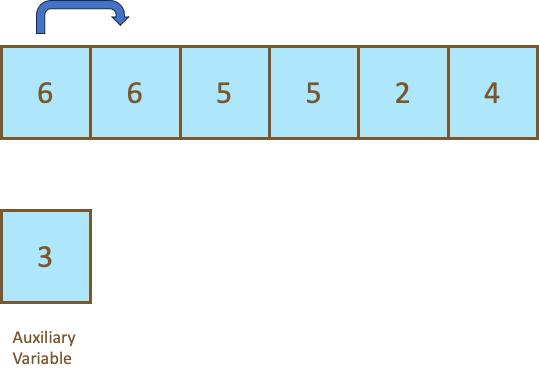
Lastly, the step 3, says that we assign the auxiliary variable to position where the first value was stored.

Now the values are swapped safely ensuring that we don’t lose any value.

If we continue traversing the list of elements and applying the Swap with Auxiliary Variable Technique, to move the largest number (in this case the 6) to the leftmost position in the lis, will end with the list of elements and the auxiliary variable like this:

In this example we move the number 6, swapping all the numbers until we have the 6 in the last position in the list of elements (leftmost), this means that the number 6 is the larger value in the list.

This is the Swap with Auxiliary Variable, what do you think about is useful? tell us your thoughts about, we see you in the next lecture.

Happy Learning!!!