The Bubble sort is the simplest algorithm to sort arrays. The goal is to sort a list of elements in the order that we need, the most of the time is the ascending order.
In this algorithm we need to iterate through a list of elements and compare a pair of adjacent elements and perform a swap of these elements if they are in the wrong order (this order can be ascending, descending or any other order that we need, to be more clear we will use the ascending order). As the algorithm traverses the list, the larger values “bubble” to the end of the list. This is why this algorithm gets its name.

Explanation of Bubble Sort
We have the next list of elements 6, 3, 5, 5, 2, 4:

Step 1
Start from the beginning of the list and compare the first pair of adjacent elements. In this case, it will be the 6 and 3. If the elements are in the wrong order (i.e., the second element is smaller than the first), swap them. To do the swap we need to use the “swap with auxiliary variable” this technique, which involves assigning one of the values to a temporary variable, assigning the second value to the first position, and then assigning the value of the temporary variable to the second position.
Step 2
Continue traversing the list, comparing and swapping for each adjacent pair until reaching the end of the list.

Step 3
Once you reach the end of the list, the largest element will be in its correct position. Repeat steps 1-3 for the remaining elements of the list, excluding the last element as it is already in its correct position.
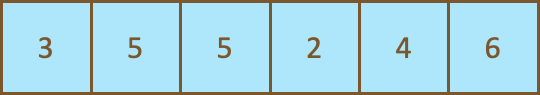
Step 4
Now repeat the step 1 to 3 until we don’t do any swap, because this means that the list of elements is sorted.
let’s show in this algorithm in Java:
| public class BubbleSort { | |
| public static int[] bubbleSort(int[] array) { | |
| //This flag indicates that our array (list of elements) is sorted, as false because we don't know if the array is sorted | |
| boolean hasChanges = false; | |
| do { | |
| //We will assign "false" because we expect the loop to finish if this flag doesn't change | |
| hasChanges = false; | |
| /*This loop is used to iterate over the array. We subtract 1 from the length because the last element does | |
| * not have any other value to compare and swap with. | |
| */ | |
| for (int x = 0; x < array.length – 1 ; x++){ | |
| /*We compare two elements: if the element at position "x" is larger than the element at position "x+1" | |
| *(the next position of the element), we need to swap the positions of those elements. | |
| */ | |
| if (array[x] > array[x + 1]) { | |
| /*We use the Swap with Auxiliary Variable technique to swap the values in the list of elements, | |
| * ensuring that no value will be lost.*/ | |
| int temp = array[x]; | |
| array[x] = array[x + 1]; | |
| array[x + 1] = temp; | |
| /*As we perform a swap or make a change in our array, the "hasChanges" variable is assigned a value | |
| * of "true" to indicate that the array is not sorted yet. | |
| */ | |
| hasChanges = true; | |
| } | |
| } | |
| } while(hasChanges == true); | |
| return array; | |
| } | |
| } |
In the line 6, we declare a variable hasChanges, that will act as a flag that indicates that our array(list of elements) is sorted. It is assigned the value of false because we don’t know if the array (list of elements) are sorted.
In line 8, we start the do-while loop to sort the array (list of elements). Once again, in the line 10, we will assign the value of "false" to the variable "hasChange" because we expect the loop to finish if this flag doesn’t change after every iteration.
In line 15, the nested for loop is used to iterate over the array. We subtract 1 from the length, because the last element does not have any other value to compare and swap with.
In line 20, We compare two elements: if the element at position x is larger than the element at position x+1 (the next position of the element that we are comparing), we need to swap the positions of those elements.
In line 23, We use the Swap with Auxiliary Variable technique to swap the values in the list of elements, ensuring that no value will be lost. In the line 29, as we perform a swap (make a change) in our array, the hasChanges variable is assigned a value of true to indicate that the array is not sorted yet.
The algorithm will continue iterating until the array don’t have any change, this will be indicated when the hasChanges flag has false after executing the nested for loop.
This solution provides a memory complexity of O(1), meaning that it does not require any additional memory beyond the input array. For the time complexity, it is O(N^2), indicating that the execution time of the algorithm grows quadratically with the size of the input.
This is the Bubble Sort algorithm, which follows the basic theory of how it should work. Essentially, we “bubble” the values towards the left position based on the desired order, whether it is ascending, descending, or any other specific order required.
Happy Learning!!!


Leave a comment